Понятия функции и графика

2) график функции растянем от оси абсцисс с коэффициентом 4, отобразим симметрично относительно оси Ox;

3) график функции сдвинем вдоль оси Oy вниз на 2 единицы.

Последний график является искомым (рис. 12).

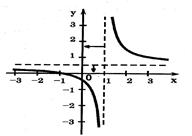
Пример 2. Построить график функции .

Снова начнем с преобразований:

.

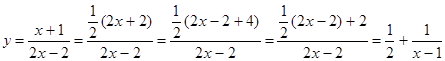Построение производится в три этапа:

1) строим график функции ;

2) переносим ось Oy влево на 1 единицу;

Рис. 13

3) затем ось Ox переносим вниз на единицы(рис. 13).

Построить графики функций.1) ;2) [18].

Письменная работа

Учащиеся выполняют письменную работу по теме «Преобразования графиков: сжатие (растяжение) графика к (от) оси абсцисс и оси ординат».

Построить графики функций. 1) ;2) .

Подведение итогов занятия

- Какое преобразование Вы использовали для построения графиков функций?

- Сформулируйте суть изученного преобразования.

Методические рекомендации к 5 и 6 занятиям. Необходимо научить передавать графически качественные особенности функций. Использовать задания различных уровней сложности, давать учащимся возможность самим конструировать задания с целью формирования интереса к изучению данного курса. Все результаты деятельности учащихся (ответы на вопросы по домашнему заданию, решение заданий на доске, активное участие в ходе всего занятия) фиксировать в индивидуальной карточке.

Тема 3. Действия над функциями

Занятие №7. Сумма (разность) функций

Цель: изучить арифметические действия (сложение, вычитание) производимые с функциями, научить учащихся строить графики функций, являющиеся суммой (разностью) других функций.

Ход занятия:

Изучение нового материала

Над функциями, как и над числами, можно производить арифметические действия, т.е. определять сумму (разность), произведение и частное функций. Графики функций , , можно получить, используя правила сложения (вычитания), умножения и деления графиков функций и . Особенно эффективным этот метод бывает в том случае, когда и являются элементарными функциями. Заметим, что осуществлять арифметические действия можно над функциями, имеющими общую область определения или общую часть областей определения. При этом частное двух функций определено, если знаменатель отличен от нуля.

Суммой двух функций и называется функция с областью определения, являющейся общей частью областей определения и , при этом значения функции равны .