Понятия функции и графика

Занятие №8. Произведение функций

Цель: изучить арифметическое действие умножение, производимое с функциями, научить учащихся строить графики функций, являющиеся произведением других функций.

Ход занятия:

Разбор домашнего задания

Разбираются задания под номерами 2), 4).

Изучение нового материала

Новый материал учитель излагает в форме лекции

Произведением двух функций и называется функция с областью определения, являющейся общей частью областей определения и , при этом значения функции равны .

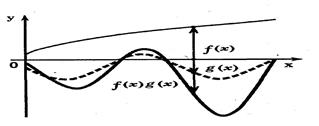
Ординаты графика произведения функций получаются путем умножения ординат графиков исходных функций соответствующих одному и тому же значению аргумента (для каждого значения аргумента из области определения произведения). Другими словами, чтобы построить график функции ,нужно построить графики функций и в одной и той же системе координат, а затем в каждой точке перемножить длины отрезков, изображающие ординаты графиков, и построить отрезок полученной длины с учетом знака произведения. Множество точек с полученными ординатами представляет график функции (рис. 16).

Закрепление полученных знаний

Пример. Построить график функции .

Функция является нечетной (она представляет собой произведение четной и нечетной функций), поэтому ее график будет симметричным относительно начала координат и его достаточно построить лишь для .

Строим графики функций и и перемножаем значения ординат этих графиков. Заметим, что в точках , в которых , функция равна нулю. В точках , где , произведение равно , т. е. эти точки лежат на прямой , а в точках , где , произведение равно , т. е. эти точки лежат на прямой (рис. 17).

Решение практических задач учащимися на занятии проводится в форме игры «Математическая рыбалка».

Для проведения игры учитель делит класс на 4команды.

Оборудование: «удочки» и «рыбки» - карточки с заданиями (на них написаны функции из второго задания).

1 задание. Сравните значения функций и , где , .