Понятия функции и графика

Решение практических задач учащимися на занятии проводится в группах.

1. Сравните значения функций и , где , .

2. Построить график функции: .

Подведение итогов занятия

- Какую тему мы изучили сегодня на занятии?

- Что называется частным двух функций?

Постановка домашнего задания

Построить график функции: .

Составить две функции, являющиеся частным других функций, и построить их графики.

Методические рекомендации к 7, 8, 9 занятиям. Необходимо научить передавать графически качественные особенности функций. Введение арифметических операций с функциями производится неявно, так как они в большинстве случаев связаны с одноименными арифметическими числовыми операциями, поэтому важно сделать осознанным перенос действий из одной области в другую, рассматривая задания в которых требуется сравнить значения функций и , и , и . Все результаты деятельности учащихся фиксировать в индивидуальной карточке.

Занятие №10. Функции, содержащие операцию «взятие модуля»

Цель: познакомить учащихся с основными приемами построения графиков функций, содержащих модуль, закрепить изученный материал в ходе выполнения упражнений. Привлечь внимание к эстетической стороне данного вида деятельности. Предусмотреть возможность творчества учащихся.

Ход занятия:

Изучение нового материала

Теоретический материал учитель рассказывает с примерами, подробно разбирая их на доске.

Иногда в формулу, задающую некоторую функцию, входит знак модуля. Приведем ряд приемов, позволяющих облегчить построение графиков функций в этом случае.

1) Построение графика функции .

=

Следовательно, график функции состоит из двух графиков: - в правой полуплоскости, - в левой полуплоскости.

Исходя из этого, можно сформулировать правило.

График функции получается из графика функции следующим образом: при график сохраняется, а при график отображается симметрично относительно оси OY .

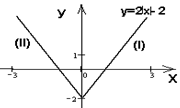Учитель разбирает примеры на доске.

Пример 1. Построить график функции .

Построение.

1) Строим график функции для ;

Рис. 19

2) достраиваем часть графика для , симметрично построенной относительно оси OY (рис. 19).