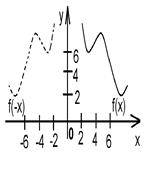
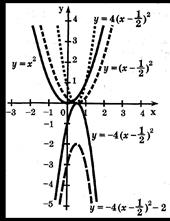
Понятия функции и графика

Занятие №6. Сжатие (растяжение) графика к (от) оси ординат

Цель: изучить преобразование графиков функций при помощи сжатия (растяжения) графика к (от) оси ординат, научить учащихся строить графики функций, используя данное преобразование.

Ход занятия:

Разбор домашнего задания

Разбираются задания, вызвавшие затруднения у учащихся, в данном случае учитель может разобрать некоторые задания по своему усмотрению.

Изучение нового материала

Изложение нового материала проводится в форме лекции.

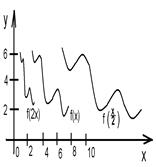Пусть требуется построить график функции , где . Рассмотрим функцию , которая в произвольной точке принимает значение . Ясно, что функция принимает такое же значение в точке , координата которой определяется равенством или , причем это равенство справедливо для всех значений из области определения функции. Но тогда график функции оказывается сжатым к оси ординат (при ) или растянутым от (при ) оси ординат относительно графика функции .

Рис. 11

Рассмотрим функцию . Легко заметить, что функции , и , принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Поэтому для построения графика функции нужно построить график функции и отразить его относительно оси ординат (рис. 11).

Соединяя предыдущие рассуждения этого пункта с последним правилом, можно строить график функции для любого знака [20].

Закрепление полученных знаний

Учитель рассматривает на конкретных примерах, как строятся графики функций, для которых применимы изложенные приемы.

Пример 1. Построить график функции.

Сначала приведем исходное выражение функции к более удобному виду:.

Затем проведем следующие построения:

1) график функции сдвинем вправо вдоль оси Ox на ;