Понятия функции и графика
Задание 2. Задает ли данная зависимость какую-нибудь функцию ![]() .
.
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]() ; 5)
; 5)![]() .
.
Подведение итогов занятия
- Какую тему мы изучили сегодня на занятии?
- Какие способы задания функции Вы знаете?
Оцените свою работу на занятии по 5-ти бальной шкале и поставьте соответствующую оценку в карточку результатов деятельности (учитель просит учащихся поднять руки: … кто оценил свою работу на уроке на «5», «4», «3»).
Постановка домашнего задания
Найдите: а) область определения функций, заданных графически и аналитически; б) множество значений функций 3), 4), 9), 10), 11).
Задайте функции: а) 10), 11)аналитически; б)1),4)графически.
1)![]() ;2)
;2)![]() ;3)
;3) ![]() ;4)
;4)![]() ;5)
;5)![]() ; 6)
; 6) ![]() ;7)
;7) ![]() ;8)
;8) ![]() [9].
[9].
|
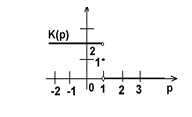
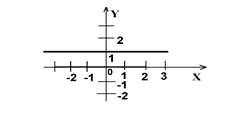 9) 10) 11)
9) 10) 11)
Методические рекомендации. При рассмотрении способов задания функции важно сформировать представление об однозначности соответствия аргумента и определенного по нему значения функции. Важным методическим приемом при изучении данной темы являются задания перевода функции из одной формы представления в другую [15]. На этапе закрепления знаний применяется индивидуальная форма обучения учащихся. Все результаты деятельности учащихся (выступление с докладом, ответы на вопросы по домашнему заданию, решение заданий на доске, активное участие в ходе всего занятия) фиксируются в индивидуальной карточке.
Тема 2. Преобразования графиков
Занятие №3. Перенос вдоль оси ординат
Цель: изучить преобразование графиков функций при помощи переноса вдоль оси ординат, научить учащихся строить графики функций, используя данное преобразование.
Ход занятия:
Разбор домашнего задания
Разбираются задания, вызвавшие затруднения у учащихся, в данном случае учитель может разобрать некоторые задания по своему усмотрению. Если вопросов нет, то проверяются ответы у наиболее сложных заданий.
Изучение нового материала
Графическое изображение функции дает весьма наглядное представление о поведении функции в целом. Нередко график оказывает существенную помощь при решении задачи. Поэтому важно уметь упрощать процедуру построения графиков, используя для этого различные преобразования.
Иногда график строится с помощью полного исследования функции, которое устанавливает область определения, промежутки убывания и возрастания, промежутки знакопостоянства, асимптоты и т.д. Но довольно часто при построении графиков функций можно избежать подобных исследований, используя ряд приемов, позволяющих путем некоторых преобразований получить график требуемой функции из графика какой-нибудь хорошо известной функции.
В качестве мотивирующей задачи для изучения нового материала учащимся предлагается выполнить задание: «Задан график функции ![]() (
(![]() ). Построить на этом же чертеже график функции
). Построить на этом же чертеже график функции ![]() (
(![]() )».
)».
Смотрите также:
Профильное обучение в рамках удовлетворения современного социального заказа
общества на профессии
Начало XXI характеризуют динамичные преобразования в теории и практике отечественного образования, явившиеся продолжением не менее динамичных преобразований в экономическом, социальном и культурном развитии общества. Увеличение и интеллектуализация направлений профессиональной деятельности, формиро ...
Понятия здоровье сберегающих технологий, функции, принципы работы,
классификация
Основной вопрос, который встает перед системой образования: как обеспечить сохранение, укрепление и восстановление здоровья учащихся? Но чтобы ответить на этот вопрос и успешно решать его, необходимо понять собственно условия жизни человека. Образование – культура – здоровье являются фундаментально ...
Концептуальные основы проблемного обучения
Концепция проблемного обучения, как и любая другая педагогическая концепция, при ее формулировке неизбежно раскрывает субъективные особенности сознания, предпочтения педагога или исследователя. Именно поэтому в педагогической литературе даются различные определения этого понятия, в той или иной мер ...
Приёмы и методы запоминания

На протяжении всей человеческой истории люди пытались придумать способы, с помощью которых они могли бы по возможности прочно усвоить какие-либо знания. С древнейших времён тема и техника запоминания занимала пытливые умы, рассматривалась и систематизировалась великими людьми прошлого.
Категории
- Главная
- Профильное обучение учащихся
- Технологии дистанционного обучения
- Формы организации обучения
- Интуиция педагога
- Мышление дошкольников
- Теория проблемного обучения
- Педагогика
- Карта сайта
- Поиск по сайту

