Понятия функции и графика

Общее правило построения графика при произвольном : строим график функции и переносим его вдоль оси ординат на единиц вниз при или вверх при или строим график функции и переносим ось абсцисс на единиц вверх при b>0 или на единиц вниз при [20].

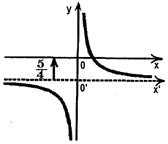Пример 1. Построить график функции .

1) Построим сначала график функции ;

2) затем перенесем ось абсцисс на единиц вверх в системе координат x’O’y;

Рис. 4

3) в новой системе координат хOу получим график функции (рис. 4).

Закрепление полученных знаний

Учащиеся индивидуально выполняют задания с последующей проверкой на доске.

1. Построить графики функций.

1) ;2) ;3) ;4) ;5) .

Учитель разбивает класс на группы (6-8 человек).

2. Для развития творческой активности учитель предлагает составить каждой группе учащихся по одному заданию (составить функцию и построить ее график) на практическое применение изученного материала. Затем группы обмениваются заданиями и решают их с последующим обсуждением.

Подведение итогов занятия

- Какое преобразование Вы использовали на занятии для построения графиков функций?

- Сформулируйте суть изученного преобразования.

Постановка домашнего задания

Построить графики функций.

1) ;2) ;3) ;4) ;5) .

Методические рекомендации. Для изучения нового материала целесообразно использовать индуктивный метод обучения, так как проведение таких рассуждений хорошо усваивается учащимися. Учитель может разделить класс на группы и каждой группе дать свой график функции. Все результаты деятельности учащихся (ответы на вопросы учителя по домашнему заданию, решение заданий на доске, активное участие в ходе всего занятия) фиксируются в индивидуальной карточке.

Занятие №4. Перенос вдоль оси абсцисс

Цель: изучить преобразование графиков функций при помощи переноса вдоль оси абсцисс, научить учащихся строить графики функций, используя данное преобразование.

Ход занятия:

Разбор домашнего задания

Разбор заданий под номерами 2), 5).

Учащиеся по желанию выходят к доске и строят графики функций с комментированием своих действий.

Изучение нового материала

Новый материал учитель излагает в форме лекции, по ходу изложения отвечая на возникающие вопросы. Учащиеся внимательно слушают и делают записи в тетрадях.

Пусть требуется построить график функции . Рассмотрим функцию , которая в некоторой точке принимает значение . Очевидно, что функция примет такое же значение в точке , координата которой определяется из равенства , т.е., причем такое равенство справедливо для всех значений из области определения функции.