Методические приемы, направленные на изучение законов и свойств арифметических действий

Следующий урок был посвящен сочетательному свойству сложения.

Тема. «Сочетательное свойство сложения. Скобки».

Цели. Познакомить с сочетательным свойством сложения, с новым математическим знаком – скобками; совершенствовать устные и письменные вычислительные навыки табличного сложения и вычитания однозначных чисел в пределах 20 с переходом через разряд.

Актуализация знаний

У. Пойдем по лесной тропинке так, чтобы не беспокоить обитателей леса, – только со стороны будем наблюдать за ними.

Игра «Распутай клубок»

На доске записаны равенства, в которых часть чисел закрыта геометрическими фигурами:

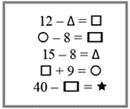
По команде учителя дети записывают на индивидуальных экранах пропущенное число и дают объяснение своим действиям.

У. Откуда начнем распутывать клубок? Почему?

Дети. Начнем с выражения 15 – 8, так как известны два числа.

У. Внимание! Напишите на своих экранах значение разности чисел 15 и 8.

Дети написали 7 и одновременно все подняли свои экраны.

– А теперь на какое равенство обратим внимание?

Д. На первое. Там кроме числа 12 изображен такой же треугольник, а значит, должно быть число 7.

У. Верно. Уменьшите 12 на 7.

На экранах дети написали число 5.

– Как нам дальше распутать клубок?

Д. Посмотрим на четвертое равенство, так как там кроме числа 9 изображен такой же квадрат, что и в первом равенстве. Значит, на нем должно быть написано число 5.

У. Верно. Найдите значение суммы чисел 5 и 9.

На экранах дети написали число 14.

Д. Возьмем второе равенство, так как там кроме числа 8 есть такой же круг, что и в четвертом равенстве. Значит, на нем должно быть написано число 14.

У. Верно. Найдите значение разности 14 и 8.

На экранах дети написали число 6.

Д. Возьмем пятое равенство, так как там кроме числа 40 есть такой же прямоугольник, что и во втором равенстве. Значит, на нем должно быть написано число 6.

У. Верно. Найдите значение разности чисел 40 и 6.

На экранах дети написали число 34.

III. Знакомство с новым материалом

У. Лесная тропинка привела нас на полянку. Осмотримся. Около деревьев – ковер из разноцветных листьев. У каждого из вас на столе кленовые листочки с заданием. Двое учеников будут работать по заданиям с обратной стороны доски.

Догадайтесь, по какому правилу записаны равенства слева и справа, и вставьте числа в «окошки».

Учащиеся выполняют задание самостоятельно.

9 + 1 + 6 = 10 + 6

7 + 3 + 2 = 10 + 2

8 + 2 + 5 = . + .

9 + 1 + 7 = . + .

9 + 1 + 6 = 9 + 7

7 + 3 + 2 = 7 + 5

8 + 2 + 5 = . + .

9 + 1 + 7 = . + .

– Посмотрим, как выполнили задание ребята, работавшие у доски. Что вы можете сказать о содержании заданий?

Д. У всех задания одинаковые.

У. А как они их выполнили?

Д. По-разному.

У. Почему так получилось?

Д. Не все разгадали правило: один знает больше, а другой меньше. Такое задание мы выполняем в первый раз.

IV. Формулировка темы урока

У. Проанализируем равенства и выясним, кто выполнил задание правильно. Сравним левые части равенств первого и второго столбиков.

Д. Они одинаковые. Складываем три числа.

У. Сравним правые части равенств первого и второго столбиков.

Д. В первом столбике сначала сложили первые два числа, а потом прибавили третье.