Методические приемы, направленные на изучение законов и свойств арифметических действий

Изучение законов и свойств арифметических действий мы рассматривали при изучении действий сложения и вычитания в концентре «Сотня».

Рассмотрим, как происходило знакомство с законами и свойствами арифметических действий .

Цель:

воспроизведение ЗУН по порядку действий в числовом выражении, умение применить переместительное свойство сложения;

создать затруднение в индивидуальной деятельности.

Учитель: Прочитайте выражения на доске и найдите их значения устно.

(11+7)-(3+6)

(635+198)+2

13+16+19+25+31+34+37

12-(5+2) +4

(178+597)+3

Уч-ся на индивидуальных досках пишут значения выражений.

Учитель: Прочитайте первое выражение? Назовите результат.

Уч-ся: Из суммы 11 и 7 вычитается сумма 3и6. Разность равна 9»

Учитель: Прочитайте второе выражение? Назовите результат.

Уч-ся: Из 12 вычитаем сумму 5 и 2 и к разности прибавляем 4, сумма равна 9.

Учитель: Прочитайте третье выражение? Назовите результат.

Уч-ся: Сумма выражения 13+16+19+25+31+34+37 равна 175.

Учитель: Как вы нашли сумму? Чем пользовались? Какой прием использовали?

Уч-ся: От перестановки слагаемых сумма не меняется.

Лена и Алеша показывают свою работу: (13+37)+ (16+34) + (19+31) +25+175! Замечательно.

Учитель: Прочитайте следующие выражения? Назовите результат.

Уч-ся: В выражении «к сумме чисел 635 и198 прибавляется 2.

Учитель: (подводящий диалог) Что вам показалось трудным? (нахождение суммы в скобках )

Как выполнила решения Катя:35+98=133 133+2=135 и 35+ (98+2)=135

Какое решение вам больше понравилось? Почему? Как в математике называют такие действия –рационально, проще. Итак, у нас две гипотезы

1-я: можно вычислить выражение по порядку действий и получить результат.

2-я: можно изменить порядок действий и получить тот же результат.

Какая из них верная и предстоит нам сегодня решить.

Учитель: Сегодня мы будем говорить о рациональном способе сложения чисел.

Постановка проблемы

Цель: постановка проблемы, самоопределение учащихся.

Учитель: А что мы с вами взяли девизом нашего урока? Будем пробовать! Искать! Давайте искать решение!

Достаточно ли нам его в нашем выражении? Нужен другой закон, позволяющий нам быстро вычислять 35+(98+2)=35+100=135.

Учитель: Чем отличаются наши выражения?

35+(98+2)=35+100=135

(35+98)+2=135

Уч-ся: Пользовались переместительным свойством сложения и поставили скобки.

Учитель: А для чего вы их использовали?

Уч-ся: Так быстрее вычислять.

Учитель: Молодцы! ВЫ думали, вы пробовали, вы объединили удобные слагаемые для нахождения суммы. (открывается тема урока – «Свойства сложения»)

Табличка: a+b=b+a (переместительное свойство сложения)

Итак, в числовом выражении у нас все получилось. А как быть с буквенными выражениями?

Посмотрите на эти выражения: (а+в)+с и а+(в+с), сравните их, используя схемы.

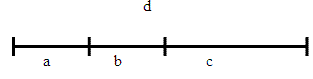
Учитель: Сейчас вы будете работать в парах, помогите друг другу сравнить эти выражения, выясните, что общего в этих выражениях и почему целое обозначено одной буквой. А сумма частей найдена по-разному.

(учащиеся на индивидуальных карточках составляют выражения, по графическим моделям)