Методические приемы, направленные на изучение законов и свойств арифметических действий

39 – 30

4. Составь с числами 10 7 19 17 16 6 9 верные числовые равенства

5. Можно ли утверждать, что значения выражений в каждой паре одинаковы?

62 + 8 84 + 6 49 + 1; 68 + 2 86 + 4 41 + 9

6. Сравни выражения и поставь знак >, <, =, чтобы неравенства были верными.

96 – 3…38 – 2 90 – 50…43 – 2

57 – 3…25 + 30 74 + 20…98 – 3

7. 30 см – 3 см…2 дм 6см

13 см + 6 см…2дм

2 дм 6см… 3дм

8. У Коли 12 марок, а у Саши на 3 марки больше. Обозначь отрезками марки Коли и Саши. Построй отрезок, который будет показывать, сколько марок у Коли и Саши вместе.

На одной полке 35 книг, на другой - 15 книг. Построй отрезки и покажи, на сколько больше книг на первой полке.

Покажем еще приемы работы над свойствами арифметических действий.

Тема: Сложение и вычитание без перехода через десяток

На этих уроках мы продолжали знакомить детей с устными и письменными приемами сложения и вычитания двузначных чисел без перехода через десяток: 60 + 24, 56 – 20, 56 – 2, 23 + 15, 69 – 24.

Важно, чтобы учащиеся хорошо усвоили, что при выполнении сложения и вычитания в столбик десятки пишут под десятками, а единицы — под единицами. С этой целью мы использовали задания на моделирование рассматриваемых алгоритмов действий с помощью разнообразного счетного материала, в которых требуется объяснить по рисунку, как выполнили действия.

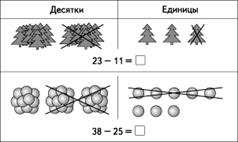
Такие задания способствуют лучшему усвоению изучаемых приемов вычислений, овладению умениями обосновывать действия и интерпретировать их с помощью наглядного материала.

На столах у детей пучки палочек (по 10 палочек) и палочки россыпью. — Отложим на счетных палочках число 35. (Дети откладывают 3 десятка и 5 единиц.)

— А сейчас прибавьте к 35 число 2. (Дети прибавляют 2 палочки.)

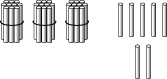
— Куда вы положили 2 палочки — к пучку или палочкам россыпью? (К палочкам россыпью.)

— Пучки палочек — это .? (Десятки.)

— Палочки россыпью — это .? (Единицы.)

— Число 2 — это .? (Единицы.)

— Что вы сделали, если говорить на языке терминов? (К единицам прибавили единицы.)

— Сколько получилось всего палочек? (37.)

— Запишем решение этого примера на доске:

— Какой можно сделать вывод? (Единицы складывают с единицами.)

— Откройте учебник на с. 24 и объясните по рисунку, как выполнено сложение. Почему ответы получились одинаковыми? (Дети объясняют.)

Письменные способы решения примеров 35 + 2 и 2 + 35 учитель показывает на доске, объясняет, как записывать числа при сложении столбиком. Учащиеся записывают примеры в тетрадях

Фрагмент 5

Тема: Сложение и вычитание с переходом через десяток

— У меня в руках красивые яблоки. (Учитель показывает картинки, на которых изображены яблоки. На обороте каждой картинки записан пример.) Мы можем подарить их белочке, если правильно вычислим ответы. (Учитель поочередно переворачивает каждое яблоко, а учащиеся решают примеры и записывают их в строчку в тетрадях.)