Методические приемы, направленные на изучение законов и свойств арифметических действий

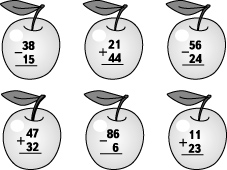
— Прочитайте ответы, которые у вас получились. (23, 65, 32, 79, 80, 34.) Какое число лишнее? Почему? (80 — круглое число, а все остальные числа не круглые.)

— Запишите эти числа в порядке убывания. (Дети записывают на следующей строчке ряд чисел: 80, 79, 65, 34, 32, 23.)

— У меня есть еще одно яблоко. (Учитель показывает картинку.)

— Чем оно отличается от других яблок? (Оно отличается цветом и формой. Это яблоко красное и круглое, а остальные яблоки желтые и продолговатые.)

— Прочитайте пример, записанный на красном яблоке. (Учитель переворачивает картинку, и учащиеся читают пример.)

— Красный цвет обозначает «Внимание!». Как вы думаете, почему этот пример выделен красным цветом? (Мы такие еще не решали.)

— А чем интересен этот пример? (Если сложить отдельные единицы, то получится 10.)

— Сколько всего десятков в числе 32? (3 десятка.) Сколько отдельных единиц в этом числе? (2 единицы.)

— С помощью палочек отложите на парте число 32. (Дети откладывают 3 десятка и 2 единицы.)

— А сейчас прибавьте к 32 число 8. (Дети прибавляют 8 палочек.)

— Куда вы положили 8 палочек — к пучкам по 10 палочек или к палочкам россыпью? (К палочкам россыпью.)

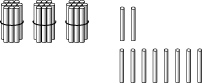
— Что вы сделали, если говорить на языке терминов? (К единицам прибавили единицы.)

— Сколько получилось палочек россыпью? (10.)

— Свяжем 10 палочек в пучок. Получим еще один десяток палочек.

— Сколько всего десятков палочек у нас получилось? (4 десятка палочек.) Сколько всего палочек? (40.)

— Запишем решение этого примера на доске:

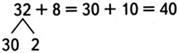
— Какой можно сделать вывод? (Если сумма единиц равна 10, то один десяток прибавляем к десяткам.)

— Откройте учебник на с. 38 и объясните по рисунку, как выполнено сложение. (Дети объясняют.)

Письменные способы решения примеров 26 + 4 и 3 + 47 учитель показывает на доске, объясняет, как записывать числа при сложении столбиком. Учащиеся записывают примеры в тетрадях.

Также мы применяли и игры.

Игра «Математическое лото»

Учитель прикрепляет на доску рисунок бочонка с цифрой 1. Дети садятся парами.

У. Итак, пришло время начинать игру. Удачи всем игрокам! Какое задание скрывается за первым бочонком?

Д. Решение круговых примеров.

Каждая пара достает из конвертов карточки с заданиями и решает круговые примеры.

56 + 3

59 – 20

39 + 3

42 + 8

50 – 2

48 + 30

78 + 5

83 – 50

33 + 7

40 – 23

17 + 9

26 + 30

У. Молодцы! Подумайте и скажите, по какому признаку можно разделить данные числовые выражения на две группы?

Д. В один столбик все суммы, а в другой все разности.

– В один столбик выражения, в которых все компоненты – двузначные числа, а в другой остальные.

У. Вы блестяще справились с этим заданием. Надеюсь, вы сможете так же удачно справиться со всеми последующими и выиграть главный приз нашей игры! Выполняя каждое последующее задание, вам необходимо будет фиксировать полученные результаты в игровом билете.