Научно – методические идеи Ф.В. Филипповича

При помощи таких конкретных задач можно одолеть и другие методические трудности в начале учения о производной, вроде, например, того, что: 1) отношение двух бесконечно малых может быть равно конечному; и 2) предел отношения при приближении Δх к нулю для данной зависимости между у и х может быть вычислен.

Аналогично выше приведенному [изложению] и задача о направлении касательной к параболе и т.п. должна показать учащимся, как можно подойти к производной с геометрической точки зрения. Графически изображая какую-нибудь математическую функцию (например, у=х2) и определяя направление касательной при помощи тангенса угла, образуемого касательной с осью х, ученики приходят к заключению, что истинная скорость изменения ординат кривой в какой-нибудь точке равна угловому коэффициенту касательной.

Сравнивая на частных случаях и числовых примерах полученные результаты: угловой коэффициент

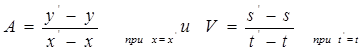
т.е.,

мы должны из этого извлечь в чистом математическом виде понятие о производной. Следовательно, после разнообразных частных примеров и применений производных, мы обобщаем понятие о производной в виде формулы

Авторы русских учебников начинают антипедагогично понятие о производной, т.е., с конца: дают определение производной при помощи отношения , а потом следуют примеры на отыскание производной и дифференциала.

Итак, общее методическое положение, по моему мнению, целесообразно и здесь, при прохождении учения о производной: «Сначала применение, а затем уже правило».

Что касается последовательности изложения элементов интегрального исчисления и целесообразности включения в школьный курс понятия определенного интеграла, то автор книги обуславливает это хотя бы тем, что интегральное исчисление дает более эффективные и экономичные методы для подсчета объемов и площадей: «Усилие, требующееся для того, чтобы ознакомиться с производной и интегралом и с тем, как при помощи этих удивительных орудий можно вычислять поверхности и объемы, будет не столь значительным, как те усилия, которые приходится делать для установления равновеликости прямой и наклонной призм или двух пирамид, и затем эти невыносимые объемы тел вращения. По сей день я не знаю выражения объема тела, получающегося при вращении сегмента круга около его диаметра .

Уже и теперь во многих новых немецких и французских учебниках по геометрии убраны громоздкие и схоластические теоремы об объемах пирамид, тел вращения и т.д. Вместо них включены в геометрию метод истощения или закон Кавальери. Так, например, в новом учебнике геометрии Бореля-Штеккеля теоремы об объемах пирамид изложены методом истощения. На русском языке в элементарном курсе геометрии Д. В. Ройтмана измерения объемов некоторых тел проходятся при помощи закона Кавальери. В самом деле, «закон Кавальери», обогативший математику и начинающий собою новую эпоху величайших открытий, сделанных в новейшее время, также удобный для определения площадей и объемов тел. Он заменял собою в течение 50-ти лет с большим успехом интегральное исчисление и поэтому тоже может в курсе геометрии сослужить роль пропедевтики для интегрального исчисления».

В результате автор приходит к выводу, что в первую очередь следует познакомить учащихся с понятием определенного интеграла, а затем неопределенного. Причем, он считает, - с введением строгой дефиниции определенного интеграла на первых порах спешить не стоит.

«С педагогической точки зрения не будет никакой ошибки, если в самом начале не давать точного определения интеграла. Я придерживаюсь того взгляда, что сначала надо определять интеграл как площадь, и лишь когда учащиеся познакомятся с ним побольше, надо дать более точное определение. На основании своей практики позволю сообщить вам, как я подхожу к определенному интегралу.

Сначала ученики чертят прямоугольник с основанием (а-b) на оси X и высотой с на оси У. Разбивая этот прямоугольник на большое число прямоугольников с основанием δх и высотой с, мы получаем, что площадь его выражается следующей формулой:.