Сравнительный анализ методики ознакомления сравенствами

Рассматривается и буквенно-графическая модель:

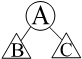всем хорошо знакомые “лучики”, используемые традиционной школой для изображения состава числа.

Введение знаков для обозначения целого и частей дает ребенку возможность относительность этих понятий. Во-первых, дети должны понять, что пока над величиной не производишь никакого действия – нельзя установить, является она (величина) частью или целым, т.е. одна и та же величина может быть частью по отношению к одной величине и она же является целым по отношению к другой.

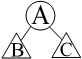Например:

Теперь величину В разобьем еще на 2 части К и Д, по отношению к которым В – целое.

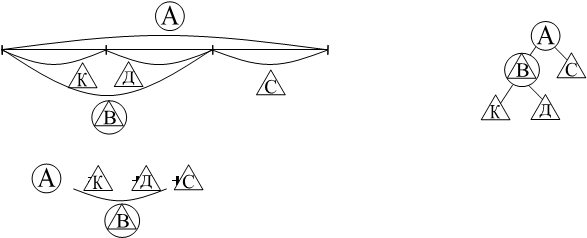Величина В по отношению к А является частью, а по отношению к величинам К и Д является целым. Наложение знаков и , друг на друга позволяет лучше увидеть относительность этого понятия.

Итак, понятие “целое” и “часть” – это относительные понятия; основное свойство этого отношения: целое не может быть меньше части, или часть не может быть больше целого. Сравнивать части между целым и остальными частями.

Умение изображать графически и описывать с помощью формул отношение частей и целого даст возможность решать целый класс текстовых задач с буквенными данными путем составления уравнений. Решив таким образом задачу, ребенок вместо букв подбирает подходящие числа и тем самым осознает, какова область допустимых значений букв не только по отношению к выполнимости арифметического действия, но и по отношению к реальности сюжета и к собственному опыту оперирования с числом. Такой подход позволяет учителю обнаружить “слабые” места у детей и незамедлительно приступить к коррекции.

Если же задача предложена с числовыми данными, то прежде чем ее решать, необходимо “восстановить”, какой она могла быть до того, как вместо букв дети из другого класса (или автор учебника) подобрали (придумали), как им кажется, подходящие числа. Это значит, что, прежде чем приступить к решению задачи, нужно установить, говоря языком математики, входят ли числовые данные в область допустимых значений по отношению к реальности сюжета. Другими словами, дети должны оценить, соответствуют ли данные числа смыслу задачи, ее сюжету, а затем заменить числа буквами и, решив задачу, вместо букв данные числа. Восстановление исходной (буквенной формы задания) текстовой задачи ставит перед детьми новую проблему: заменять одинаковые числа одинаковыми буквами или разными? Ответ на такой вопрос с неизбежностью потребует более глубокого осмысления текста задачи и тех понятий, которые составляют ее смысл.

С помощью заданий в разделе “Проверь себя!” вы сможете составить сначала проверочную работу, а затем и контрольную (контрольная работа по данной теме подводится не сразу по завершении ее изучения, а после рассмотрения следующей!)

2.6. Что такое уравнение?

Система РО.

Описание методики работы над построением и решением уравнений рассмотрим с рассмотрения различных определений уравнения.

В школьной энциклопедии уравнение определено как “два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестным. Решить уравнение – значит найти все те значения неизвестных (корни или решения уравнения), при которых оно обращается в верное равенство или установить, что таких значений нет”. Там же дано определение уравнения как “аналитической записи задачи о разыскивании значений аргументов, при которых значения двух функций равны”.

Понятно, что под аналитической записью и понимается запись равенства, левая или правая части которого содержат неизвестную (неизвестные) букву (или число). Именно буквенное выражение определяет функцию от входящих в него букв, заданную на допустимых числовых значениях.

Введение записи задачи (о нахождении неизвестной величины) с помощью уравнения начинается с конкретной задачи. Способы составления и решения уравнений опираются на отношение целого и его частей, а не на 6 правил нахождения неизвестных при сложении, вычитании, умножении, делении.