Сравнительный анализ методики ознакомления сравенствами

Если дети скажут, что этого мало, то долейте заметно больше, чем нужно (или отлейте больше, чем нужно). Именно тогда дети и смогут осмыслить то, что речь идет об определенном количестве – ни больше, ни меньше.

Возникает новая задача: какое количество воды нужно долить, чтобы стало поровну?

Невозможность восстановить прежний объем есть основание для рождения у детей о метках на обеих банках.

Поскольку дети уже умеют изображать величины, то предложите им сначала изобразить данные величины (объемы воды или количество воды) с помощью схемы, обозначив их буквами.

Затем, запишем формулы: А>B или B<A.

Теперь ответ на вопрос (сколько же нужно долить воды?) может быть показан на банках и на схеме: 1) на банках: от метки на одной банке до метки на другой или с помощью двух меток на одной банке, если вторая метка прикреплена детьми при сравнении:

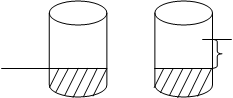
Метка, которую добавили

Метка дети, на том же уровне, что

и на первой банке

На схеме эту же разность (разницу) дети могут показать так:

это тот объем воды, который нужно долить

А в банку с меньшим объемом (В).

Помните! Не банка В, а объем воды

В в банке – это В, банки то одинаковые.

Показать то, сколько нужно долить воды, – это то же самое, что узнать, на сколько одна величина больше другой или меньше другой, – А>В (на С). Чтобы узнать эту новую величину С, нужно от большей величины отнять меньшую, т.е. С = А – В.

Значит, если к величине В добавить разницу, а “настоящие математики” говорят “разность”, – величину С, равную А – В, то получится величина, равная А.

А = В + С (1) или А = В + (А – В) (2)

С

Найти эту разницу, т.е. разность между величинами и записать формулу (2) дети смогут лишь после введения знака “минус”.

Чтобы изменить отношение между величинами, т.е. из неравенства сделать равенство или, наоборот, из равенства сделать неравенство (но таких заданий мало, т.к. они являются обратными, восстанавливающими неравные величины из равных, поэтому их желательно дополнить), нужно будет одну из двух величин либо увеличить (+), либо уменьшить (–), а может быть уменьшить одну и увеличить другую, причем на сколько уменьшают одну, на столько же увеличивают другую.

Очень важно, чтобы дети понимали: когда они от неравенства переходят к равенству, то отнимать или добавлять нужно не сколько угодно, а определенное количество, соответствующее разности этих величин.

Работа с графическими и знаковыми моделями, т.е. схемой и формулой, является основным звеном в цепи решения учебной задачи.

Отношение неравенства однородных величин (А<В) и операция сложения (А+В=С) обладают следующими свойствами:

Каковы бы ни были А и В, имеет место одно и только одно из трех отношений: или А=В, или А<В, или В<А.

Если А<В и В<С, то А<С (транзитивность отношений “меньше”, “больше”).

Для любых двух величин А и В существует однозначно определенная величина С=А+В.

А+В = В+А (коммуникативность сложения).

А+(В+С) = (А+В)+С (ассоциативность сложения).

А+В >А (монотонность сложения).

Если А>В, то существует одна и только одна величина С, для которой В+С=А (возможность вычитания).

Изучение свойств отношений, о которых шла речь, открывает перед ребенком новые возможности.

Как из частей составить целое

Введение об отношении частей и целого понятия обусловлено, прежде всего необходимостью обучения ребенка решению текстовых задач (прямых и косвенных) алгебраическим способом, т.е. на основе составления уравнений. Для этого ребенок должен научится изображать это отношение с помощью схем, опираясь на которые он сможет описать это особое отношение величин, не зависящее от их конкретного числового значения, в виде буквенных формул. Сформировав это понятие, дети приобретают умение выражать целое через части и части через целое:

И , где

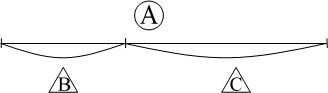кружками обозначено целое, а треугольником – части. Графической моделью этого отношения могут служить разные геометрические фигуры (круг, прямоугольник, треугольник и др.), но наиболее удобным и простым способом изображения этого отношения является отрезок.