Этапы решения задач с помощью уравнений

Поиск пути решения заканчивается составлением плана решения задачи. Под планом решения будем понимать объяснение того, что узнаем, выполнив то или иное действие, и указание по порядку выполнения арифметических действий. Приведем пример поиска решения задачи аналитическим путем.

Пример. В трех школах 1072 ученика, во второй на 16 учеников больше, чем в третьей, и на 14 учеников меньше, чем в первой. Сколько учеников в каждой школе?

Краткая запись задачи показана на рисунке.

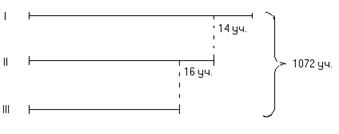
Поиск пути решения. Чтобы определить число учащихся в каждой школе, надо сначала узнать число учащихся в одной из школ и разность между этим числом учащихся других школ.

В условии дана разность числа учащихся второй и третьей школ и разность числа учащихся первой и второй школ. Поэтому в первую очередь удобнее определять число учащихся второй школы; для этого приравниваем число учащихся первой и третьей школ к числу учащихся второй школы. Чтобы узнать, сколько было бы учащихся в трех школах, если бы в каждой школе было столько, сколько во второй, надо знать настоящее число учащихся трех школ (дано в условии) и на сколько учеников оно увеличится или уменьшится при предполагаемом изменении числа учащихся первой и третьей школ. Последнее число определим, зная, что число учащихся первой школы надо уменьшить на 14 учеников (чтобы уравнять со второй школой), а число учащихся третьей школы увеличить на 16.

План решения.

На сколько учеников увеличилось бы общее число трех школ, если бы в каждой школе число учеников было бы таким же, как во второй?

Сколько учеников было бы в трех школах, если бы число учеников в каждой школе было бы таким же, как во второй школе?

Сколько учеников во второй школе?

Сколько учеников в первой школе?

Сколько учеников в третьей школе?

Во втором случае (синтетический путь) решающий выделяет в тексте задачи два каких-либо данных и на основе связи между ними, установленной при анализе, определяет, какое неизвестное может быть найдено по этим данным и с помощью какого действия. Затем, считая полученное число данным, решающий опять выделяет два взаимосвязанных данных и определяет, какое неизвестное может быть найдено по ним и с помощью какого действия, и т.д., пока выполнение очередного действия не приведет к определению искомого.

Пример. У трех братьев была некоторая сумма денег: у первого и второго вместе 600 р., у второго и третьего вместе 500 р., у третьего и первого 700 р. Сколько денег было у каждого брата в отдельности?

Решение. Краткая запись задачи показана на рисунке.

I и II - 600 р.

II и III - 500 р.

I и III - 700 р.

Сколько денег было у каждого брата в отдельности?

Поиск пути решения. Зная, что у первого и второго братьев вместе 600 р., а у второго и третьего вместе 500 р., можем найти, на сколько денег у первого брата больше, чем у третьего.

По сумме и разности денег первого и третьего узнаем, чему равно удвоенное количество денег третьего брата, а затем, сколько денег имеет каждый из них. После этого можно найти, сколько денег у второго.

План решения.

На сколько рублей у первого брата больше, чем у третьего?

Чему равно удвоенное количество денег третьего брата?

Сколько денег имел третий брат?

Сколько денег имел первый брат?

Сколько денег имел второй брат?

При решении задач анализ и синтез в рассуждениях, как правило, переплетаются. Осуществляя поиск пути решения задачи синтетически, анализ часто производят «про себя». В то же время, каким бы приемом мы не вели поиск пути решения составной задачи, ее предварительный анализ (хотя бы подсознательный) неизбежен.