Этапы решения задач с помощью уравнений

Деятельность по решению задачи включает следующие этапы независимо от выбранного метода решения:

анализ содержания задачи;

поиск пути решения задачи и составление плана её решения;

осуществление плана решения задачи;

проверка решения задачи.

Поясним это на конкретных примерах, выделяя отдельно каждый из названных этапов.

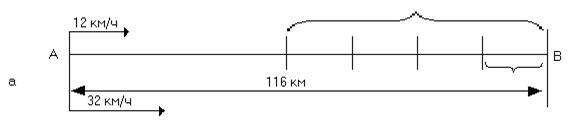
Пример. Расстояние от пункта А до пункта В равно 116 км. Из А в В одновременно отправляются велосипедист и мотоциклист. Скорость велосипедиста 12 км/ч, скорость мотоциклиста – 32 км/ч. Через сколько часов велосипедисту останется проехать в четыре раза больший путь, чем мотоциклисту?

Решение.

Анализ задачи.

В задаче идет речь о велосипедисте и мотоциклисте, которые отправляются одновременно в одном направлении из пункта А в В. Известно, что расстояние от А до В равно 116 км, скорость велосипедиста – 12 км/ч, скорость мотоциклиста – 32 км/ч. Требуется узнать, через сколько часов велосипедисту останется проехать в четыре раза больший путь, чем мотоциклисту.

Краткая запись задачи (в виде схематического чертежа) показана на рисунке 1а.

Поиск пути решения задачи и составление плана ее решения.

Обозначим искомое число часов через х. Зная скорость мотоциклиста, можем узнать, какое расстояние он проедет за х ч, а затем, зная расстояние между пунктами А и В, найдем, какое расстояние останется проехать мотоциклисту до пункта В.

Зная скорость велосипедиста, можем узнать, какое расстояние он проедет за х ч, а затем найдем, какое расстояние ему останется проехать до пункта В.

По условию велосипедисту останется проделать путь, в четыре раза больший, чем мотоциклисту. Следовательно, мы можем составить уравнение, приравняв между собой путь, в четыре раза больший пути, который осталось проехать мотоциклисту.

Решив этот уравнение, найдем, через сколько часов велосипедисту останется проделать путь, в четыре раза больший, чем мотоциклисту.

Осуществление плана решения задачи.

Пусть через х ч велосипедисту останется проделать в четыре раза больший путь, чем мотоциклисту. За это время мотоциклист проедет 32х км, значит, ему останется проехать до пункта В (116 – 32х) км. Велосипедист за х ч проедет 12х км, значит, ему останется проехать до пункта В (116 – 12х) км (рис. б). По условию это расстояние в четыре раза больше, чем расстояние, которое останется проехать мотоциклисту. Следовательно, получаем уравнение

(116 – 32х) · 4 = 116 – 12х.

После несложных преобразований будем иметь:

464 – 128х = 116 – 12х 116х = 348 х = 3.

Итак, искомое решение равно 3 ч.

Проверка решения задачи.

Через 3 ч мотоциклист проедет 32 · 3 = 96 (км), останется 116 – 96 = 20 (км). Через 3 ч велосипедист проедет 12 · 3 = 36 (км), останется до конца 116 – 36 = 80 (км). Найдем, во сколько раз велосипедисту останется сделать больший путь, чем мотоциклисту: 80 : 20 = 4 (раза). Расхождения с условием задачи нет. Задача решена правильно.

Ответ: через 3 ч велосипедисту останется сделать в четыре раза больший путь, чем мотоциклисту.

Выделенные этапы представляют норму деятельности человека по решению задач. В реальном процессе решения задачи этапы не имеют четких границ, и человек, решающий задачу, не всегда выделяет их в явном виде, переходя от одного к другому незаметно для себя. Вместе с тем решение каждой отдельно взятой задачи обязательно должно содержать все указанные этапы, осмысленное прохождение которых (вместе со знанием приемов их выполнения) делает процесс решения любой задачи осознанным и целенаправленным, а значит, более успешным. Игнорирование одних этапов (например, поиска пути решения) может привести к решению методом «проб и ошибок», игнорирование других (например, проверки решения задачи) – к получение неверного ответа и т.д.