Сущность и структура решения текстовых задач

Итак, весь процесс решения задачи можно разделить на восемь этапов:

1-й этап – анализ задачи;

2-й этап – схематическая запись задачи;

3-й этап – поиск способа решения задачи;

4-й этап – осуществление решения задачи;

5-й этап – проверка решения задачи;

6-й этап – исследование задачи;

7-й этап – формулирование ответа задачи;

8-й этап – анализ решения задачи.

Приведенная схема дает лишь общее представление о процессе решения задач как о сложном и многоплановом процессе. Приведем пример решения задачи, показав конкретно этот процесс.

Лодка прошла по течению реки расстояние между двумя пристанями за 6 ч, а обратный путь она совершила за 8 ч. За сколько времени пройдет расстояние между пристанями плот, пущенный по течению реки?

Анализ задачи.

В задаче речь идет о двух объектах: лодка и плот. Лодка имеет какую-то собственную скорость, а река, по которой плывет и лодка, и лот, имеет определенную скорость течения. Именно поэтому лодка совершает путь между пристанями по течению реки за меньшее время (6 ч), чем против течения (8 ч). Но эти скорости (собственная скорость лодки и скорость течения реки) в задаче не даны (они неизвестны), так же как неизвестно расстояние между пристанями. Однако требуется найти не эти неизвестные скорости и расстояния, а время, за которое плот проплывет неизвестное расстояние между пристанями.

Схематическая запись задачи.

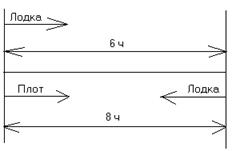
Поиск способа решения задачи.

Нужно найти время, за которое плот проплывает расстояние между пристанями А и В. Для того чтобы найти это время, надо знать расстояние АВ и скорость течения реки. Оба они неизвестны, поэтому обозначим расстояние АВ буквой s (км), а скорость течения реки примем равной а км/ч. Чтобы связать эти неизвестные с данными задачи (время движения лодки по и против течения реки), нужно еще знать собственную скорость лодки. Она тоже неизвестна, положим, что она равна V км/ч. Отсюда естественно возникает план решения, заключающийся в том, чтобы составить систему уравнений относительно введенных неизвестных.

Осуществление решения задачи.

Итак, пусть расстояние АВ равно s км, скорость течения реки а км/ч, собственная скорость лодки V км/ч, а искомое время движения плота на пути в s км равно х ч. Тогда скорость лодки по течению реки равна (V + a) км/ч. За 6 ч лодка, идя с этой скоростью, прошла путь АВ в s км. Следовательно,

6 (V + a) = s

Против течения эта лодка идет со скоростью (V - a) км/ч и путь АВ в s км она пройдет за 8 ч, поэтому

8 (V - a) =s

Наконец, плот, плывя со скоростью а км/ч, покрыл расстояние s км за х ч, следовательно,

ах = s

Уравнения (1), (2), (3) образуют систему уравнений относительно неизвестных s, а, V и х. Так как требуется найти лишь х, то остальные неизвестные постараемся исключить.

Для этого из уравнений (1) и (2) найдем:

V + а = , V – a = .

Вычитая из первого уравнения второе, получим:

2а = - , отсюда а = .