Изучение порядковой структуры

Сформулируем ведущие дидактические положения, на которые может и должно опираться изучение порядковой структуры.

I. Необходимость пропедевтики. Поскольку понятие упорядоченного множества является весьма абстрактной структурой, обобщающей целый ряд конкретных математических объектов, для усвоения этого понятия важна подготовительная работа - повторение соответствующего изученного материала и его систематизация, подробный разбор примеров на отношение порядка.

II. Принцип фундаментальности подразумевает научность излагаемого знания, т. е. четкость определений и формулировок, строгость доказательств, «разметку» границ данной математической теории, его связи и приложения.

III. Принцип наглядности. Наглядность порядковых понятий и интерпретаций способствует усвоению абстрактного материала. Важную роль играет изображение конечных упорядоченных множеств диаграммами Хассе.

IV. Тренинг. Изучение порядковой структуры должно сопровождаться самостоятельным решением разнообразных упражнений: проверочных тестов, заданий учебного характера, учебно-исследовательских и научно-исследовательских задач.

V. Внутриматематические связи. Математика - единая наука, разные разделы которой связаны содержательно и структурно. Имеется тесная взаимосвязь между основными типами математических структур, установленная еще П.С. Александровым, М. Стоуном, Г. Биркгофом. Особенно хорошо эти связи прослеживаются на конечных объектах.

VI. Прикладные возможности. Порядковая структура, являясь одной из самых фундаментальных дискретных структур математики, входит в состав математических основ компьютерных наук. Компьютерная алгебра и компьютерная графика усиливают возможности применения аппарата теории упорядоченных множеств в самых разных областях науки и практики.

Что следует знать преподавателю математики о порядковой структуре?

Во-первых, исходные порядковые понятия, включая точные грани, виды упорядоченных множеств, в частности упорядоченные множества с условием минимальности (они служат носителем индуктивных рассуждений, допускают нетерову индукцию), решетки, булевы алгебры, упорядоченные группы, кольца и поля.

Во-вторых, модельные примеры: цепь действительных чисел с обычным порядком, булеаны, решетка натуральных чисел с отношением делимости. Эти примеры хорошо иллюстрируют обобщающий характер порядкового подхода. Полезно научиться изображать конечные упорядоченные множества диаграммами Хассе, что особенно важно в дискретной математике. Надо понимать, что алгебры высказываний, множеств и событий являются булевыми алгебрами, а множество всех действительнозначных функций на произвольном множестве образует дистрибутивную решетку с поточечно определенным отношением порядка.

В-третьих, определенный минимум фактов: простейшие свойства упорядоченных множеств, принцип двойственности, эквивалентность порядкового и алгебраического понятий решетки, теорема Стоуна о строении конечных булевых алгебр, теорема Тарского о неподвижной точке, лемма Кенига, формулировки леммы Цорна и теорем Цермело и Гельдера, порядковые свойства основных числовых систем.При обучении математике студентов и учащихся физико-математических лицеев желательно систематически использовать порядковый язык, находить и применять информацию об упорядоченных структурах.

Таблица модельных примеров упорядоченных множеств

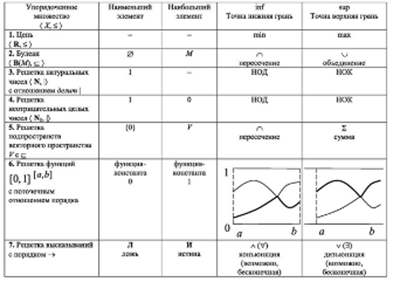
Возможная последовательность изучения порядковой структуры:

1. Повторение теоретико-множественных понятий.

2. Рассмотрение модельных примеров упорядоченных множеств (примеры из нижеследующей таблицы).

3. Определение исходных порядковых понятий.

4. Конечные упорядоченные множества и их диаграммы Хассе.

5. Отработка порядковых понятий на модельных примерах, их иллюстрация таблицами и графами, на диаграммах Эйлера - Венна и Хассе.

6. Доказательство простейших свойств упорядоченных множеств. Принцип двойственности.

7. Построение новых примеров и контрпримеров.

8. Понятие решетки. Эквивалентность порядкового и алгебраического определений.

9. Начала теории решеток. Понятия подрешет- ки, идеала, конгруэнции, гомоморфизма, фактор-решетки, прямого произведения решеток.

10. Дистрибутивные решетки. Их свойства и представления.

11. Булевы решетки, булевы алгебры и булевы кольца.

12. Исследовательские задачи об упорядоченных множествах и решетках. Темы курсовых и дипломных работ. Примерные задачи и темы работ можно найти в.

Пункты 1-11 сопровождаются решением учебных упражнений.