Изучение порядковой структуры

Для проверки сюръективности f возьмем произвольное непустое множество B = {a1, ., ak} атомов решетки L. Нужно найти элемент b е L, для которого f(b) = B. Положим b = a1 + . + ak. Ясно, что B с f(b). Если a е f(b), т. е. a # b, то a = a(a1 + . + ak) = aa1 + . + aak. Отсюда следует, что атом a совпадает с одним из атомов а, иначе aa1 + . + aak = 0. Поэтому и f(b) с B, т. е. f(b) = B.

Наконец, если x # у, то f(x) с f(y) по определению отображения f. Обратно, если f(x) с f(y) для x, у е L, то по доказанному x = Ef(x) # Ef(y) = у. Следовательно, биекция f является (порядковым) изоморфизмом решеток L и B(A), что завершает доказательство теоремы.

Булеан B(M) является булевой алгеброй относительно операций объединения, пересечения и дополнения. Пусть B - произвольная булева алгебра с бинарными операциями +, • и унарной операцией'.

Упомянутая классическая теорема Стоуна утверждает, что B изоморфна подалгебре булеана B(M), где в качестве M можно взять множество всех максимальных идеалов в B. Элементы и операции в B интерпретируются соответственно как подмножества в M и теоретико-множественные операции над ними.

Так, равенство ab = 0 в алгебре B означает, что соответствующие множества не пересекаются. Мы уже знаем, что B является (булевой) решеткой с отношением порядка # (a # b означает a + b = b), интерпретируемым как отношение включения с подмножеств множества M. После этого становится ясно, что булевы алгебры действительно должны обладать естественные свойствами (1) - (5).

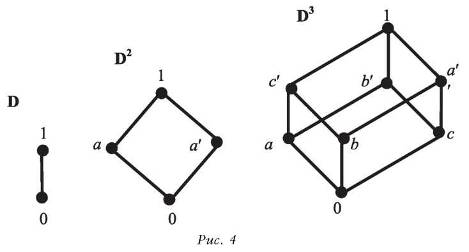
В заключение рассмотрим обобщение примера 6, показывающее возможность дальнейших исследований в теории решеток. Для данных непустого множества X и решетки S рассмотрим решетку Sx всевозможных отображений X^S с поточечно определенными операциями сложения и умножения отображений. Если решетка S имеет наименьший элемент 0 и не содержит делителей нуля, то равенство fg = 0 (здесь 0 трактуется как функция-константа, принимающая в любой точке множества X значение 0) в решетке функций Sx означает, что f(x) = 0 или g(x) = 0 для каждого x е X. Знакомая картина получается в случае Rx для числовых промежутков X, когда функции изображаются графиками. В теории пучковых (функциональных) представлений абстрактная ограниченная дистрибутивная решетка S представляется как решетка сечений соответствующего пучка ограниченных дистрибутивных решеток-слоев Sx, индексированных точками базисного топологического пространства X. Слои должны быть устроены проще исходной решетки S. На этом пути получается и сформулированная выше классическая теорема Стоуна, когда все Sx изоморфны двухэлементной цепи.